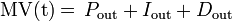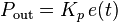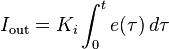PID control discussion
PID control discussion
Educate me!! :-)
I realise the wikipedia has a good page here : http://en.wikipedia.org/wiki/PID_controller
If anyone would care to comment on anything related to this at all, specifically about real world aspects of limitations and quirks and implementation that would be excellent.
In addition, this search could provide some interesting reading for some of you : http://www.google.com/search?hl=en&q=smith%20predictor
What have you got?
Thanks in advance,
Admin.
I realise the wikipedia has a good page here : http://en.wikipedia.org/wiki/PID_controller
If anyone would care to comment on anything related to this at all, specifically about real world aspects of limitations and quirks and implementation that would be excellent.
In addition, this search could provide some interesting reading for some of you : http://www.google.com/search?hl=en&q=smith%20predictor
What have you got?
Thanks in advance,
Admin.
DIYEFI.org - where Open Source means Open Source, and Free means Freedom
FreeEMS.org - the open source engine management system
FreeEMS dev diary and its comments thread and my turbo truck!
n00bs, do NOT PM or email tech questions! Use the forum!
The ever growing list of FreeEMS success stories!
FreeEMS.org - the open source engine management system
FreeEMS dev diary and its comments thread and my turbo truck!
n00bs, do NOT PM or email tech questions! Use the forum!
The ever growing list of FreeEMS success stories!
-
thebigmacd
- LQFP112 - Up with the play
- Posts: 205
- Joined: Thu Apr 10, 2008 5:51 pm
Re: PID control discussion
I've got no knowledge on the Smith Predictor, but I deal with PID all the time.
Firstly, 99% of the time, forget about the D part. A PI controller is all you really need to deal with.
Secondly, error = ideal - actual.
The Proportional part of a PI controller is very simple, the farther the value is from ideal, the more output you apply to counteract the error. This component is just Kp * Error, where Kp is the "proportional gain" or constant of proportionality that determines how much output you are going to apply for a given amount of error. If Kp = 1, for every 1 unit of error, the output will be 1. This determines how sensitive to error the controller will be. If Kp is high, the output is going to change a lot for very small variations in the error. Depending on how the output actually affects the system (direct or inverse action), Kp will be positive or negative. The inverse of Kp, 1/Kp is called the Proportional band, and is generally used where the output is bounded in terms of 0% and 100%.
The Integral part of a PI controller is simple as well, you just take a total error of all the samples in the past and multiply them by a constant Ki. This adds an offset to the output that accounts for steady-state constant error once equilibrium is reached with the P portion. Remember, this is not an average, but a SUM of all previous values of error. If the output is physically unable to cause the system to reach the desired value due to a jam or lack of power or a disconnect, this component will "wind up" quite quickly and cause a lot of problems.
For PI control, OUT = Kp*err + Ki*sum_err
Now, in discrete space which is what our microprocessors operate in, this can be greatly simplified by using only the current and previous error sample and not maintaining a sum. I won't go there quite yet.
If you think about the response of a controller to error as a line on a graph in the form y = mx + b, y is the output, m is Kp, x is error, and b is Ki*tot_err.
Firstly, 99% of the time, forget about the D part. A PI controller is all you really need to deal with.
Secondly, error = ideal - actual.
The Proportional part of a PI controller is very simple, the farther the value is from ideal, the more output you apply to counteract the error. This component is just Kp * Error, where Kp is the "proportional gain" or constant of proportionality that determines how much output you are going to apply for a given amount of error. If Kp = 1, for every 1 unit of error, the output will be 1. This determines how sensitive to error the controller will be. If Kp is high, the output is going to change a lot for very small variations in the error. Depending on how the output actually affects the system (direct or inverse action), Kp will be positive or negative. The inverse of Kp, 1/Kp is called the Proportional band, and is generally used where the output is bounded in terms of 0% and 100%.
The Integral part of a PI controller is simple as well, you just take a total error of all the samples in the past and multiply them by a constant Ki. This adds an offset to the output that accounts for steady-state constant error once equilibrium is reached with the P portion. Remember, this is not an average, but a SUM of all previous values of error. If the output is physically unable to cause the system to reach the desired value due to a jam or lack of power or a disconnect, this component will "wind up" quite quickly and cause a lot of problems.
For PI control, OUT = Kp*err + Ki*sum_err
Now, in discrete space which is what our microprocessors operate in, this can be greatly simplified by using only the current and previous error sample and not maintaining a sum. I won't go there quite yet.
If you think about the response of a controller to error as a line on a graph in the form y = mx + b, y is the output, m is Kp, x is error, and b is Ki*tot_err.
Keith MacDonald
Control Engineering (Systems) Technologist
Control Engineering (Systems) Technologist
Re: PID control discussion
I messed with this a bit in college, and have been reading up on it some recently having no end of issues with the MegaSquirt's impersonation of the PID controller. I remember never having serious trouble setting one up before, but suddenly they are the worst thing I've ever used. Z-transform is french for "boot in your neither regions". Just ask Jean, he's from Canada, he probably knows French. 
Int_Term = Previous_Error + Ki * Current_Error
verses
Int_Term += Ki * Current_Error
OUT += Kp*err + Ki*sum_err
This is driving me SO batty. The way I wrote it is how the MS does it. They say it makes sense, but I don't buy it!
If you have a simple P controller, it integrates.
If I'm approaching my target, my output gets bigger not smaller, ensuring massive overshoot.
The other way to look at it is this:
What does all this mean? It means when your idle is low, or your boost is low, your control valve continues to open even as you approach the target. It ensures you'll never get into the 'steady offset' case where a purely proportional controller should be.
And it ensures that tuning it is an utterly black art. The recommendation of the folks who wrote that code:
If you half the time period, completely retune the controller, there is no way to just adjust the values to get the same response.
A TRUE PID controller would mean you either wouldn't change anything (absolute time reference) or you would leave Kp alone, and only half/double the Ki and Kp terms if you only considered time in loop-execution steps.
I guess the intelligent thing to do is to recompile my own version of the code with the proper math in there, tweak all the constants and scale factors (of numbers like 100,000) they put in to make it function, and see how it goes.
As it is, it would minimally need a lot of prediction. Of course, since the control doesn't go negative, I'd have to define a 'neutral' position, I think. So instead of OUT = sum(error_terms), it would be like OUT = sum(error_terms) + 50%, though really were it me, I'd choose that number to be the steady state number that works (28% for me), but I think I'm making this more complicated than it needs to be.
Or, I'm terribly misunderstanding something.
I'm curious, why is this easier? Something like:thebigmacd wrote: Now, in discrete space which is what our microprocessors operate in, this can be greatly simplified by using only the current and previous error sample and not maintaining a sum. I won't go there quite yet.
Int_Term = Previous_Error + Ki * Current_Error
verses
Int_Term += Ki * Current_Error
Ok, just to be very clear here.... You didn't meanthebigmacd wrote: For PI control, OUT = Kp*err + Ki*sum_err
OUT += Kp*err + Ki*sum_err
This is driving me SO batty. The way I wrote it is how the MS does it. They say it makes sense, but I don't buy it!
If you have a simple P controller, it integrates.
If I'm approaching my target, my output gets bigger not smaller, ensuring massive overshoot.
The other way to look at it is this:
More there than I needed, but you end up with, towards the end, an infinite sum over time.AbeFM wrote:I guess I don't know what this "z-transform" thing is. But using wiki's terms:PID controller theory
Note: This section describes the ideal parallel or non-interacting form of the PID controller. For other forms please see the Section "Alternative notation and PID forms".
The PID control scheme is named after its three correcting terms, whose sum constitutes the manipulated variable (MV). Hence:
where Pout, Iout, and Dout are the contributions to the output from the PID controller from each of the three terms, as defined below.
Proportional term
The proportional term makes a change to the output that is proportional to the current error value. The proportional response can be adjusted by multiplying the error by a constant Kp, called the proportional gain.
The proportional term is given by:
Where
* Pout: Proportional output
* Kp: Proportional Gain, a tuning parameter
* e: Error = SP − PV
* t: Time or instantaneous time (the present)
However, using the '+=', you get something differnet, and for discussion, let's again drop the I, D terms:
MV(t) = MV(t-1) + Kp*E(t) + Ki (=0) + Kd(=0)
MV(t) = MV(t-1) + Kp*E(t)
MV(t) = MV(t-2) + Kp*E(t-1) + kp*E(t)
MV(t) = (Sum over i = 0 to t) Kp*E(t)
MV(t) = kp * (Sum over i = 0 to t) E(t)
That looks an aweful lot like:
which, to my mind, makes it the integral term. For that matter, the I term becomes a double integral, and the D term cancels since it's the integral of a derivative (or think about adding something with a different sign every time? Sorta a stretch there).
Anyway, I'm going to go try it on the bench, but I must be missing something really big in this "z-transform" thing, because the P term should be timescale insensitive to first order.
What does all this mean? It means when your idle is low, or your boost is low, your control valve continues to open even as you approach the target. It ensures you'll never get into the 'steady offset' case where a purely proportional controller should be.
And it ensures that tuning it is an utterly black art. The recommendation of the folks who wrote that code:
If you half the time period, completely retune the controller, there is no way to just adjust the values to get the same response.
A TRUE PID controller would mean you either wouldn't change anything (absolute time reference) or you would leave Kp alone, and only half/double the Ki and Kp terms if you only considered time in loop-execution steps.
I guess the intelligent thing to do is to recompile my own version of the code with the proper math in there, tweak all the constants and scale factors (of numbers like 100,000) they put in to make it function, and see how it goes.
As it is, it would minimally need a lot of prediction. Of course, since the control doesn't go negative, I'd have to define a 'neutral' position, I think. So instead of OUT = sum(error_terms), it would be like OUT = sum(error_terms) + 50%, though really were it me, I'd choose that number to be the steady state number that works (28% for me), but I think I'm making this more complicated than it needs to be.
Or, I'm terribly misunderstanding something.
Re: PID control discussion
Yeah, French is my first language. But the accent here is not the same as in France (both in French and English) so you'd be more likely to get a D-transform here than a Z-transform.8InchesFlacid wrote:Z-transform is french for "boot in your neither regions". Just ask Jean, he's from Canada, he probably knows French.
Now back to the serious discussion...
Re: PID control discussion
LOL :-) At least french canadians don't blow up green peace boats... ;-)
DIYEFI.org - where Open Source means Open Source, and Free means Freedom
FreeEMS.org - the open source engine management system
FreeEMS dev diary and its comments thread and my turbo truck!
n00bs, do NOT PM or email tech questions! Use the forum!
The ever growing list of FreeEMS success stories!
FreeEMS.org - the open source engine management system
FreeEMS dev diary and its comments thread and my turbo truck!
n00bs, do NOT PM or email tech questions! Use the forum!
The ever growing list of FreeEMS success stories!
-
thebigmacd
- LQFP112 - Up with the play
- Posts: 205
- Joined: Thu Apr 10, 2008 5:51 pm
Re: PID control discussion
Okay here goes:
PID Programming
The Z-transform of 1 times a function is 1, or Z^0
The Z-transform of the integral of a function is 1 / (1 - Z^-1)
The Z-transform of the derivative of a function is (1 - Z^-1)^2 / (1 - Z^-1)
This gives us a transfer function of:
Output/Error = Kp * 1 + Ki * (1 / (1 - Z^-1)) + Kd * ((1 - Z^-1)^2 / (1 - Z^-1))
We then multiply through to remove the bottom term of the fractions. Multiply through by (1 - Z^-1)
Output/Error * ((1 - Z^-1)) = Kp * (1 - Z^-1) + Ki + Kd * (1 - Z^-1)^2
Output/Error * 1 - (Output/Error * Z^-1) = Kp - (Kp * Z^-1) + Ki + Kd (1 - 2Z^-1 + Z^-2)
Output/Error * 1 - (Output/Error * Z^-1) = Kp - (Kp * Z^-1) + Ki + Kd - (2 * Kd * Z^-1) + (Kd * Z^-2)
Output/Error = (Kp + Ki + Kd) - ((Kp + 2 * Kd) * Z^-1) + (Kd * Z^-2) + (Output/Error * Z^-1)
Wherever something is multiplied by one, we can replace this with Z^0, because anything ^ 0 = 1.
Output/Error * Z^0 = (Kp + Ki + Kd) * Z^0 - ((Kp + 2 * Kd) * Z^-1) + (Kd * Z^-2) + (Output/Error * Z^-1)
We then multiply through by Error
Output * Z^0 = (Kp + Ki + Kd) * Error * Z^0 - ((Kp + 2 * Kd) * Error * Z^-1) + (Kd * Error * Z^-2) + (Output * Z^-1)
See a pattern? Write it out by hand and see.
In Z space, Z^0 means NOW, Z^-1 means ONE AGO, and Z-2 means TWO AGO. We can transfer this to a program by indicating N TIMES AGO by and integer number. 0 = now, 1 = one ago, 2 = two ago, etc.
We add lines before and after to shift the data to the proper array location and we are done. As stated in the info above, Kd, Ki, and Kp change depending on the sample period. We can add the last output value by using += rather than using an array index.
Instant PID control.
PI Programming
If you start with PI only:
Output/Error = Kp * 1 + Ki * (1 / (1 - Z^-1))
You end up with:
Output/Error = (Kp + Ki) - Kp * Z^-1 + Output/Error*Z^-1
Output = (Kp + Ki) * Error * Z^0 - Kp * Z^-1 + Output * Z^-1
Which gives you the code
Which then simplifies to
In MS format, the would be
This is how a PI controller should be written.
P Control
Output/Error = Kp * Z^0
Output = Kp * Error * Z^0
This one is pretty straightforward. General rule of thumb is is there is only a proportional term, you only look at the current state [0]. If there is an integral term, you look at the last state [1] as well. If there is an integral term, you have to look two time ago [2]. Don't forget to shift your table values at the proper time and in the correct order!
PID Programming
The Z-transform of 1 times a function is 1, or Z^0
The Z-transform of the integral of a function is 1 / (1 - Z^-1)
The Z-transform of the derivative of a function is (1 - Z^-1)^2 / (1 - Z^-1)
This gives us a transfer function of:
Output/Error = Kp * 1 + Ki * (1 / (1 - Z^-1)) + Kd * ((1 - Z^-1)^2 / (1 - Z^-1))
We then multiply through to remove the bottom term of the fractions. Multiply through by (1 - Z^-1)
Output/Error * ((1 - Z^-1)) = Kp * (1 - Z^-1) + Ki + Kd * (1 - Z^-1)^2
Output/Error * 1 - (Output/Error * Z^-1) = Kp - (Kp * Z^-1) + Ki + Kd (1 - 2Z^-1 + Z^-2)
Output/Error * 1 - (Output/Error * Z^-1) = Kp - (Kp * Z^-1) + Ki + Kd - (2 * Kd * Z^-1) + (Kd * Z^-2)
Output/Error = (Kp + Ki + Kd) - ((Kp + 2 * Kd) * Z^-1) + (Kd * Z^-2) + (Output/Error * Z^-1)
Wherever something is multiplied by one, we can replace this with Z^0, because anything ^ 0 = 1.
Output/Error * Z^0 = (Kp + Ki + Kd) * Z^0 - ((Kp + 2 * Kd) * Z^-1) + (Kd * Z^-2) + (Output/Error * Z^-1)
We then multiply through by Error
Output * Z^0 = (Kp + Ki + Kd) * Error * Z^0 - ((Kp + 2 * Kd) * Error * Z^-1) + (Kd * Error * Z^-2) + (Output * Z^-1)
See a pattern? Write it out by hand and see.
In Z space, Z^0 means NOW, Z^-1 means ONE AGO, and Z-2 means TWO AGO. We can transfer this to a program by indicating N TIMES AGO by and integer number. 0 = now, 1 = one ago, 2 = two ago, etc.
Code: Select all
OUTPUT[0] = (Kp + Ki + Kd) * Error[0] - (Kp + 2 * Kd) * Error[1] + Kd * Error[2] + OUTPUT[1]
Code: Select all
Error[2] = Error[1] //Shift data by one time constant
Error[1] = Error[0] //Shift data by one time constant
Error[0] = Actual - Requested //Calculate error NOW
Alpha = Kp + Ki + Kd //Calculate Alpha constant
Beta = Kp + 2 * Kd //Calculate Beta constant
Gamma = Kd //Calculate Gamma constant
OUTPUT += Alpha * Error[0] - Beta * Error[1] + Gamma * Error[2]
PI Programming
If you start with PI only:
Output/Error = Kp * 1 + Ki * (1 / (1 - Z^-1))
You end up with:
Output/Error = (Kp + Ki) - Kp * Z^-1 + Output/Error*Z^-1
Output = (Kp + Ki) * Error * Z^0 - Kp * Z^-1 + Output * Z^-1
Which gives you the code
Code: Select all
Output[0] = (Kp + Ki)*Error[0] - Kp*Error[1] + Output[1]
Code: Select all
OUTPUT += (Kp + Ki)*Error[0] - Kp*Error[1]
Code: Select all
OUTPUT += (Kp + Ki)*Error_Now - Kp*Error_Last
P Control
Output/Error = Kp * Z^0
Output = Kp * Error * Z^0
Code: Select all
Output = Kp * Error[0]
Keith MacDonald
Control Engineering (Systems) Technologist
Control Engineering (Systems) Technologist
Re: PID control discussion
You must be good, you used italics AND bold (not just holding down shift).
Seriously, thanks for the nice write up. Here's what I noticed, aside from the obvious that Engineers start with 'the z transform blah blah' instead of what a z transform is or why you'd do it... But it's ok, I think I managed to make some sense of it anyway. And again, thanks for putting it out explicitly!
But it's ok, I think I managed to make some sense of it anyway. And again, thanks for putting it out explicitly!
Now THAT'S exactly what I've been saying all along, that the P term should be purely proportional to the current error, plus some initial 'best guess' term, chosen to be the steady state position you think it the best guess (I'd probably use the valve opening for idle that I normally set it at).
Alpha = KP
Beta = KI
Gama = KD
Or something like that, I have to look closer. But they are doing something way wrong.
The MS does this:
which boils down to:
which in turn boils down to:
That's an integral.
My questions now is how do I convince the MS guys they are wrong?
I was going to go through their code for all three terms, but wow... it's hard to read through. The more I look at it the less I care, it's wrong, so... what more do I need to know?
If I felt the guys on that board wanted to make it work right, instead of just BE right, I'd go through the trouble of fixing it.
FYI it's:
The nice part about the Z-transform is it's mathematically very cheap. I should really boil it down and make sure it does what I want (I think so), and that it takes into account all history (not just the past two time points).
Leaving actual processing cycles aside, PID looks like this (to me):
error = target - actual
time_loopstart = get_current_time()
delta_t = time_loopstart - time_lastloop
P_contribution = Kp * error
I_contribution += Ki * error * delta_t
D_contribution = Kd * (error_last - error) / delta_t
error_last = error
time_lastloop = time_loopstart
output = P_contribution + I_contribution + D_contribution
That assumes the loop gets run regularly. If not, you need to correct by the time since the last time you were run.shown underlined.
Seriously, thanks for the nice write up. Here's what I noticed, aside from the obvious that Engineers start with 'the z transform blah blah' instead of what a z transform is or why you'd do it...
As I did in other places, I want to look at what happens to just the P term, if that doesn't make sense, I think something's broken.thebigmacd wrote:Code: Select all
OUTPUT[0] = (Kp + Ki + Kd) * Error[0] - (Kp + 2 * Kd) * Error[1] + Kd * Error[2] + OUTPUT[1]
Code: Select all
OUTPUT[0] = (Kp + Ki + Kd) * Error[0] - (Kp + 2 * Kd) * Error[1] + Kd * Error[2] + OUTPUT[1]
set Ki = Kd = 0
OUTPUT[0] = Kp * Error[0] - Kp * Error[1] + OUTPUT[1] (but output1 depends on history....)
= Kp * (Error[0] - Error[1] + Error[1] - Error[2]) + OUTPUT[2] (for the dense, we'll go another step)
= Kp * (Error[0] - Error[2] + Error[2] - Error[3]) + OUTPUT[4] (carried to infinite we get)
= Kp * Error[0] + OUTPUT[initial-position]
I'll have to look, I think what happened is the MS folks are usingWe add lines before and after to shift the data to the proper array location and we are done. As stated in the info above, Kd, Ki, and Kp change depending on the sample period. We can add the last output value by using += rather than using an array index.Instant PID control.Code: Select all
Error[2] = Error[1] //Shift data by one time constant Error[1] = Error[0] //Shift data by one time constant Error[0] = Actual - Requested //Calculate error NOW Alpha = Kp + Ki + Kd //Calculate Alpha constant Beta = Kp + 2 * Kd //Calculate Beta constant Gamma = Kd //Calculate Gamma constant OUTPUT += Alpha * Error[0] - Beta * Error[1] + Gamma * Error[2]
Alpha = KP
Beta = KI
Gama = KD
Or something like that, I have to look closer. But they are doing something way wrong.
The MS does this:
Code: Select all
rpm_error = (int)targ_rpm - (int)outpc.rpm;
Kp = ((long)rpm_error * flash5.pwmidle_Kp);
tmp1 = ((long)(Kp) * (int)(flash5.pwmidle_open_duty - flash5.pwmidle_closed_duty)) /
((long)pg5_ptr->pwmidle_target_rpms[PWMIDLE_NUM_BINS - 1] * 1000);
tmp1 += IACmotor_pos;
if (tmp1 < flash5.pwmidle_min_duty) {
tmp1 = flash5.pwmidle_min_duty;
} else if (tmp1 > flash5.pwmidle_open_duty) {
tmp1 = flash5.pwmidle_open_duty;
}
IACmotor_pos = tmp1;
IACmotor_last = IACmotor_pos; Code: Select all
error = target - actual;
Kp_error = error * Kp;
tmp1 = Kp_error;
tmp1 += OUTPUT;
OUTPUT = tmp1;
Code: Select all
error = target - actual;
OUTPUT += Kp * error;
Looks like I started responding before reading everything you said, so yes we're saying the same things.PI Programming
If you start with PI only:
Output/Error = Kp * 1 + Ki * (1 / (1 - Z^-1))
(dot dot dot)
In MS format, the would beCode: Select all
OUTPUT += (Kp + Ki)*Error_Now - Kp*Error_Last
My questions now is how do I convince the MS guys they are wrong?
I was going to go through their code for all three terms, but wow... it's hard to read through. The more I look at it the less I care, it's wrong, so... what more do I need to know?
If I felt the guys on that board wanted to make it work right, instead of just BE right, I'd go through the trouble of fixing it.
FYI it's:
Code: Select all
rpm_error = (int)targ_rpm - (int)outpc.rpm;
pwmidle_error_sum += rpm_error;
if (pwmidle_error_sum > 1000) {
pwmidle_error_sum = 1000;
}
if (pwmidle_error_sum < -1000) {
pwmidle_error_sum = -1000;
}
pwmidle_deriv = rpm_error - pwmidle_last_error;
pwmidle_last_error = rpm_error;
Kp = ((long)rpm_error * flash5.pwmidle_Kp);
Ki = ((long)pwmidle_error_sum * flash5.pwmidle_Ki);
Kd = ((long)pwmidle_deriv * flash5.pwmidle_Kd);
if (IdleCtl == 6) {
tmp1 = (((long)((Kp + Ki - Kd) / 100 ) << 8) *
(int)(flash5.pwmidle_open_duty - flash5.pwmidle_closed_duty)) /
((long)pg5_ptr->pwmidle_target_rpms[PWMIDLE_NUM_BINS - 1] * 2550);
} else {
tmp1 = ((long)(Kp + Ki - Kd) * (int)(flash5.pwmidle_open_duty - flash5.pwmidle_closed_duty)) /
((long)pg5_ptr->pwmidle_target_rpms[PWMIDLE_NUM_BINS - 1] * 1000);
}
tmp1 += IACmotor_pos;
if (IdleCtl == 7 || IdleCtl == 8) {
if (tmp1 > (int)flash5.pwmidle_min_duty) {
tmp1 = flash5.pwmidle_min_duty;
} else if (tmp1 < (int)flash5.pwmidle_open_duty) {
tmp1 = flash5.pwmidle_open_duty;
}
} else {
if (tmp1 < flash5.pwmidle_min_duty) {
tmp1 = flash5.pwmidle_min_duty;
} else if (tmp1 > flash5.pwmidle_open_duty) {
tmp1 = flash5.pwmidle_open_duty;
}
}
DISABLE_INTERRUPTS;
IACmotor_pos = tmp1;
IACmotor_last = IACmotor_pos;
ENABLE_INTERRUPTS;Leaving actual processing cycles aside, PID looks like this (to me):
error = target - actual
time_loopstart = get_current_time()
delta_t = time_loopstart - time_lastloop
P_contribution = Kp * error
I_contribution += Ki * error * delta_t
D_contribution = Kd * (error_last - error) / delta_t
error_last = error
time_lastloop = time_loopstart
output = P_contribution + I_contribution + D_contribution
That assumes the loop gets run regularly. If not, you need to correct by the time since the last time you were run.shown underlined.
Re: PID control discussion
You know, thinking about this some more, I don't see why the simple version is so much more computationally expensive. The worst thing I see in it is dividing by the amount of elapsed time.
Otherwise it's a couple of multiplications and a couple of additions and the odd subtraction or two. Maybe there's some floating point issue adding a lot of time to it if the constants are less than unity, but that would be the same as the z-transform case.
The nice part about doing it the 'simple' way is nothing depends on time at all, you pick constants that work and until you get to extremes there shouldn't be an effect when changing the loop time - very handy if you only get around to running it when you get around to it.
Otherwise it's a couple of multiplications and a couple of additions and the odd subtraction or two. Maybe there's some floating point issue adding a lot of time to it if the constants are less than unity, but that would be the same as the z-transform case.
The nice part about doing it the 'simple' way is nothing depends on time at all, you pick constants that work and until you get to extremes there shouldn't be an effect when changing the loop time - very handy if you only get around to running it when you get around to it.
-
thebigmacd
- LQFP112 - Up with the play
- Posts: 205
- Joined: Thu Apr 10, 2008 5:51 pm
Re: PID control discussion
The reason we use the Z-transform is because discrete sampling is just that...discrete samples taken and processed periodically. When you take discrete samples, the analog data between samples is lost. Laplace transforms work for analog because they assume the sample frequency is infinite. As the sample frequency is reduced from infinity, the Laplace transform becomes more and more inaccurate.8InchesFlacid wrote:You must be good, you used italics AND bold (not just holding down shift).
Seriously, thanks for the nice write up. Here's what I noticed, aside from the obvious that Engineers start with 'the z transform blah blah' instead of what a z transform is or why you'd do it...But it's ok, I think I managed to make some sense of it anyway. And again, thanks for putting it out explicitly!
The critical characteristic of Z-transforms is that they inherently contain a sample period component that completely changes the K constants.
Into time space, the translation is
Z = A*e^sT
As you can see, if the sample time T is changed, the resultant function is different. In the process of getting a function into Z space, this constant T is factored out and included in the constants, such as Kp, Ki, Kd in our case. The specific math is eluding me at this time, but this is why Ki and Kd change with sample time.
Keith MacDonald
Control Engineering (Systems) Technologist
Control Engineering (Systems) Technologist
-
thebigmacd
- LQFP112 - Up with the play
- Posts: 205
- Joined: Thu Apr 10, 2008 5:51 pm
Re: PID control discussion
The only issue is that if you allow sample period to increase, the analog stuff that happens in-between can start to do some funky things with your accuracy. Z-space isn't perfect in this respect.8InchesFlacid wrote:You know, thinking about this some more, I don't see why the simple version is so much more computationally expensive. The worst thing I see in it is dividing by the amount of elapsed time.
Otherwise it's a couple of multiplications and a couple of additions and the odd subtraction or two. Maybe there's some floating point issue adding a lot of time to it if the constants are less than unity, but that would be the same as the z-transform case.
The nice part about doing it the 'simple' way is nothing depends on time at all, you pick constants that work and until you get to extremes there shouldn't be an effect when changing the loop time - very handy if you only get around to running it when you get around to it.
The long and the short of it is PID actually sucks for any system with higher than 2nd-order response. Which is pretty much anything that does not stick to a 2nd-order differential equation.
This is why we use tables for fuel; engine VE is not linear in the mathematical sense.
Keith MacDonald
Control Engineering (Systems) Technologist
Control Engineering (Systems) Technologist